Accueil > IA > Méta-Heuristiques & Algorithmes de Recherche Locale

Les Algorithmes de Recherche Locale
ou
Méta-heuristiques

[ Révision du 18/06/2000 | Version PDF ]

Afin d’entrevoir d’éventuelles pistes de solution, et en nous appuyant notamment sur [Myna97], nous allons explorer deux grandes familles de méthodes qui permettent de résoudre de manière générale des problèmes d’optimisation en variables discrètes:

• les méthodes (d'exploration) globales, en particulier l'énumération implicite heuristiquement ordonnée, que nous illustrerons au travers de l’algorithme A*,
  
  
• et les méthodes (d'exploration) locales, en particulier les méthodes d'exploration par voisinage, pour lesquelles nous étudierons le recuit simulé et la recherche tabou.

Mais ce chapitre n’aurait d’intérêt sans une orientation dans le sens de la planification : c’est donc dans l’optique de les appliquer à la planification d’actions que nous allons étudier ces différentes techniques, ce qui nous permettra de conclure sur les intérêts éventuels qu’elles sont susceptibles de présenter.

Remarque :

Tout au long de ce chapitre, on utilisera aussi bien les termes d’opérateur, de mouvement ou encore de modification pour parler des actions.

Exemple d’énumération implicite :
parcours d’arbre avec l’algorithme[1] A* 

Nous allons ici détailler une première approche qui permet d’obtenir une solution et qui utilise l’algorithme¹ A*. Cet algorithme a été présenté pour la première fois dans [HNR68].

Il fonctionne sur le principe de la recherche du « meilleur-d’abord » (Best first search).

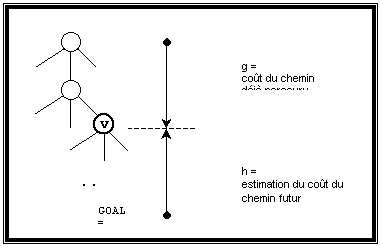
On dispose d’une situation initiale START bien connue, d’une (ou plusieurs) situation(s) finale(s) déterminée(s) GOAL. La préoccupation est alors de trouver comment passer de START à GOAL avec un coûts minimal ou un profit maximum.

On appelle état l’ensemble des informations permettant d’identifier un sous - problème. Pour passer d’un état à un autre, on dispose d’opérateurs apportant un gain additif. Appliquer ces opérateurs à un état s’appelle développer l’état. Réciproquement, on suppose qu’on dispose de marqueurs permettant de retrouver les développements successifs ayant conduit à une solution. Car c’est d’avantage le cheminement nécessaire pour identifier une solution que la solution elle même qui compte dans cette approche : cette dernière étant connue.

En fait l’algorithme parcours un arbre de recherche et, pour éviter de s’engager vers un noeud par un chemin plus mauvais qu’un précédant, il va stocker des informations sur les nœuds qu’il parcours. Pour cela, il va évaluer la qualité du nœud auquel il se trouve grâce à une fonction d’évaluation f.

Lorsque l’on examine l’état v, on connaît le coût de START à v : c’est la somme des coût c(START, v₁), c(v₁, v₂), …, c(v_k, GOAL) des opérateurs nécessaires pour passer de START à v. Mais, à moins que v = GOAL, le coût (« futur ») de v à GOAL est inconnu : on ne peut que l’estimer.

En général, la fonction d’évaluation est donc définie comme la somme de deux autres fonctions notées couramment g et h, telles que pour un nœud donné v:

·      g donne le coût du chemin déjà parcouru depuis la racine, de START à v,

·     

v

h est une estimation du coût du chemin restant à faire jusqu’au nœud final, de v à GOAL.

Figure 1 : Recherche avec l’algorithme A*

Mais on peut aussi pondérer le rapport entre le gain connu g et le gain espéré  h par la formule du type f = w.g + (1 - w).h où wÎ[0; 1].

L’idéal est d’avoir une estimation exacte de cette distance, ainsi l’effort d’exploration de l‘espace de recherche sera minimal. Cependant de telles estimations demandent souvent trop de temps de calcul pour être applicables. Il faut donc trouver un compromis entre le temps de calcul et l’exploration de l’espace de recherche pour rendre l’algorithme pratiquement acceptable [Nils82] [PeKi82].

C’est pour cela qu’on parle de stratégie informée. En effet, à tout instant, pour chaque nœud, on doit pouvoir fournir une estimation de la valeur du chemin restant à parcourir.

         Le principe de l’algorithme consiste à chaque étape à choisir un état u dans la liste A_VOIR ^(1°) des états à développer, initialement égale à START, et ce jusqu'à ce que GOAL ait été identifié, ou que cette liste soit vide (le problème n’admet pas de solution). Cette sélection suit une stratégie « meilleur d’abord », dans la mesure où l’élément sélectionné dans A_VOIR est celui dont l’évaluation est la meilleure.

On supprime u de A_VOIR pour l’ajouter à la liste DEJA_VU ^(2°), initialement vide, qui contient l’ensemble de tous les états parcourus pendant la recherche.

Par application d’opérateurs sur l’état sélectionné u, on obtient de nouveaux états v_i, les successeurs de u, que l’on ajoute à la liste A_VOIR ^(3°).

Si ces situations v_i ont déjà été envisagées, mais avec un coût  moindre, on met les coût à jour, et on considère que l’état doit être réexaminé en tenant compte de cette nouvelle situation.

Cela donne de manière plus formelle :

1.        Fonction A_star(START, GOAL : T_Data) : T_Path
2.                        A_VOIR ← {START}                      // Liste des éléments à développer
3.                        DEJA_VU ← Æ                                 // Liste des éléments déjà explorés
4.                        u ← Æ
5.                        Tant que (A_VOIR ≠ Æ) et (u ≠ GOAL) faire
6.                                           v ← Choix_dans(A_VOIR)          // En meilleur d’abord
7.                                           Si (u ¹ G) alors
8.                                                              A_VOIR ← A_VOIR \ {u}
9.                                                              DEJA_VU ← DEJA_VU È {u}
10.                                                           LISTE_FILS ← Developper(u) // En appliquant les opérateurs
11.                                                           Pour chaque v dans LISTE_FILS faire
12.                                                                              Si (v Ï (A_VOIR È DEJA_VU)) alors
13.                                                                                                 A_VOIR ← A_VOIR È {(v; f(v))}
14.                                                                                                 Pred(v) ← u
15.                                                                              Sinon
16.                                                                                                 w ← Pred(v)
17.                                                                                                 Si (g(w) + c(w, v) < g(u) + c(u, v)) alors
18.                                                                                                                   Pred(v) ← u
19.                                                                                                                   g(v) ← g(u) + c(u, v)
20.                                                                                                                   f(v) ← g(v) + h(v)
21.                                                                                                                   Si (v Î DEJA_VU) alors
22.                                                                                                                                      DEJA_VU ← DEJA_VU \ {v}
23.                                                                                                                                      A_VOIR ← A_VOIR È {v}
24.                                                                                                                   Fin_Si
25.                                                                                                 Fin_Si
26.                                                                              Fin_Si
27.                                                           Fin_Pour
28.                                        Fin_Si
29.                     Fin_TantQue
30.                     Si (u = GOAL) alors
31.                                        Retourner (START, ..., Pred(Pred(u)), Pred(u), u)
32.                     Sinon
33.                                        Pas de solution
34.                     Fin_Si

L’intérêt de cet algorithme apparaît tout de suite : si un nœud a déjà été marqué précédemment, avec un coût moindre, alors l’algorithme y retourne.

Cela ce fait au détriment d’un inconvénient tout aussi flagrant qui pourrait s’avérer limitant avec des domaines étendus: la consommation excessive d’espace mémoire.

A* présente les trois propriétés suivantes :

1.      terminaison :
si le graphe est fini (nombre fini d’états) et que la fonction d’évaluation f est à valeurs positives ou nulles (f (v_i)≥0) alors A* s’arrête, soit parce qu’il a trouvé un nœud terminal, soit parce que la liste des nœuds A_VOIR est vide (tous parcourus).

2.      admissible :
si f=g+h et h(v)≥h*(v) "v (pour un problème de maximisation), alors A* est admissible, c’est à dire que l’algorithme trouve toujours une solution optimale du problème.

3.      consistant :
pour h si et seulement si quelque soit le successeur v de u, |h(v) – h(u)| ≤ c(u, v) 

La recherche étant basé sur le coût d’un nœud, la fonction d’évaluation joue un rôle clef. Comme la détermination du coût d’un chemin de la racine au nœud courant n’est pas difficile, c’est bien la fonction d’estimation h qui est le point sensible et déterminant de l’algorithme.

Comme on le constate dans l’algorithme, les « sauts en arrière » peuvent être fréquents. Or, si l’on ne veut pas être obligé de recalculer dans ces cas les valeurs déjà acquises, il faut que la fonction h soit monotone : elle n’aurait d’intérêt autrement. Concrètement, à mesure que l’on s’approche du nœud final (optimum), la fonction d’évaluation h doit varier toujours dans le même sens (croître ou décroître), et particulièrement, quand on revient à un même nœud précédemment marqué, cette fonction doit retourner une valeur cohérente avec ce principe : un même état du système en deux endroits différents du l’arbre (deux nœuds ayant la même étiquette) devront avoir la même valeur h(v). Cela permet de gérer la notion d’impasse dans un chemin.

On peut maintenant se demander comment obtenir ces valeurs de h(v) pour tous les nœuds v de l’arbre, à savoir les déterminer une seule fois de manière statique au début de l’algorithme, ou les (re)calculer de manière dynamique à chaque fois que l’on arrive à un noeud. Si le nombre d’états, de nœuds, est faible, on peut se permettre de calculer une fois pour toutes la valeur de h pour chacun de ces nœuds, puis de stocker ses valeurs, afin de les utiliser quand nécessaire surtout si le calcul de h n’est pas simple. Mais si le nombre de nœuds est important, voire dénombrable mais infini, cela devient inefficace voire impossible : il faudra alors savoir déterminer pour un nœud quelconque v, à tout moment, la valeur h(v). Cela est d’autant plus efficace, que connaître et donc calculer cette valeur h(v) pour tous les nœuds peut être une perte de temps inutile dans la mesure où il y a très souvent une partie des nœuds qui n’est pas explorée. L’idéal serait de mixer les avantages de ces deux méthodes, à savoir calculer en temps réel la valeur h en un nœud v, que lorsque l’on passe effectivement par ce nœud, puis la stocker pour le cas où l’on viendrait à repasser par un nœud portant la même étiquette.

Iterative Deepening A* (IDA*) [Korf85] est un algorithme d’exploration de graphe dérivé de A*. Son principe est le suivant :

·      A chaque itération, on réalise une exploration en profondeur d’abord.

·      Dans cette exploration, tous les états dont l’évaluation dépasse un certain seuil sont éliminés de l’exploration.

·      Ce seuil est initialement (à la première itération) égal à l’évaluation de l‘état initial.

·      A chaque nouvelle itération, le seuil est le minimum des évaluations qui dépassaient le seuil dans la dernière itération.

·      Chaque état est évalué par une fonction de la forme f = g + h comme dans A*.

·      On n’explore à chaque itération que des éléments dont l’évaluation est égale au seuil.

Cela donne de manière plus formelle:

1.        Function IDA(START, GOAL : T_Data) : T_Path
2.                      SEUIL ← f(START)
3.                      NOUVEAU_SEUIL ← -∞
4.                      u ← START
5.                      Tant que (u ≠ GOAL) ou (f(u) > SEUIL) faire
6.                                    u ← EnProfondeur(u, START, SEUIL, NOUVEAU_SEUIL)
7.                                    SEUIL ← NOUVEAU_SEUIL
8.                                    NOUVEAU_SEUIL ← -∞
9.                      Fin_TantQue
10.                   Retourner (START, ..., Pred(Pred(u)), Pred(u), u)
11.      
12.     Function EnProfondeur(u, START, s, ns : T_Data) : T_State
13.                   LISTE_FILS ← Developper(u)                   // En appliquant les opérateurs
14.                   Pour chaque v dans LISTE_FILS tant que (v ≠ GOAL) ou (f(v) < s) faire
15.                                      Si (f(v) ≤ s) alors
16.                                                         En_Profondeur(v, s, ns)
17.                                      Sinon
18.                                                         Si (f(v) < ns) alors
19.                                                                            ns ← f(v)
20.                                                         Fin_Si
21.                                      Fin_Si
22.                   Fin_Pour
23.                   Si (v = GOAL) et (f(v) ≥ s) alors
24.                                      Retourner (v)
25.                   Sinon
26.                                      Retourner (START)               // On recommence depuis START
27.                   Fin_Si

Cet algorithme améliore A* mais possède toujours certains inconvénients.

Tout d’abord, cette méthode est intéressante lorsque le graphe d’exploration n’est pas un arbre ou que ou que le nombre d’états à explorer est extrêmement grand. En effet, IDA* est asymptotiquement optimal en terme de temps de résolution et de place mémoire requise en comparaison des autres algorithmes d’énumération. Par contre, lorsque la taille du problème est raisonnable, IDA* est pénalisé par sa répétition de tâches (par exemple faite qu’une seule fois en général dans un algorithme de recherche en profondeur uniquement). Cependant les besoins en mémoire d’IDA* sont minimaux, puisque l’exploration en profondeur d’abord peut se faire de façon récursive avec un minimum de mémorisation.

Cette monotonie à propos de la notion d’estimation, garante de l’efficacité de A*, est en fait une limite, dans la mesure où, contrairement à d’autre méthodes comme celles que nous allons voir dans les prochains chapitres, elle empêche d’emprunter un chemin qui serait tout d’abord plus coûteux, mais finalement (sur 2 ou 3 niveaux) bien plus avantageux : A* exclue les chemins localement défavorables.

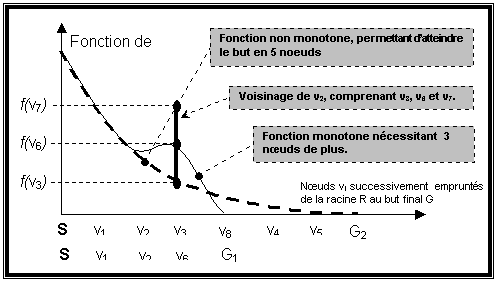Figure 2 : Fonctions coût monotone et non monotone

L’énumération implicite présente l’avantage de fournir des garanties fortes sur les résultats trouvés. La structure de recherche systématique se prête particulièrement bien à l’élaboration de propriétés de la forme théorème/preuve. On a donc des garanties concernant le caractère optimal de la solution trouvée, le nombre d’états explorés, etc.

Cependant, cette sécurité sur le déroulement de l’algorithme et la qualité des résultats a un prix. Ces algorithmes nécessitent un temps de calcul très important, et sont assez peu souples. Dans de nombreux cas, un temps de calcul assez important est nécessaire avant qu’une solution, même de mauvaise qualité, puisse être fournie par l’exploration. En général, l’énumération implicite requiert une place mémoire importante. Il s’agit d’une seconde limitation majeure aux performances de tous ces algorithmes.

Cet algorithme fourni donc un chemin optimum de parcours d’arbre. Dans la figure précédante, avec la fonction monotone, la solution est la séquence de nœuds (S, v₁, v₂, v₃, v₄, v₅, G₂).

…

On obtient donc comme solution, une séquence totalement ordonnée, ce qui n’est pas la meilleure des choses, comme nous l’avons précédemment expliqué.

L’exploration locale

         En réponse à cette monotonie, nous allons maintenant explorer les métaheuristiques d’exploration locale.

Les métaheuristiques sont des méthodes caractérisées par l’absence de garantie sur le caractère optimal ou même l’écart à l’optimum des solutions approchées trouvées. Il s’agit d’une logique de recherche d’un élément satisfaisant en parcourant de manière déterminée, orientée, l’ensemble à explorer.

Parmi toutes ces techniques, présentées et étudiées dans [GlGr89], nous allons nous intéresser seulement aux algorithmes d’exploration locale, car ils sont également liés à une représentation du problème sous forme de graphe. Mais ces algorithmes présentent plus de degrés de liberté que ceux de l’énumération implicite.

Au niveau des composantes, il faut distinguer deux niveaux :

·      la détermination du voisinage, le choix d’un élément, et la mémorisation, comme caractéristiques générales présentent sous une forme ou une autre dans les différents algorithmes,

·      la  diversification, l’intensification et l’oscillation dont l’efficacité est reconnue, mais la présence non obligatoire.

Le principe fondamental de l’exploration locale est, à partir d’une solution totalement instanciée, de passer à un autre élément, du même type que cette solution mais différent, et de recommencer de proche en proche.

Dans un premier temps, nous allons donc approfondir l’expression « élément de même type » ou élément voisin.

Le voisinage défini les éléments proches vers lesquels on peut porter l’exploration, mais il ne contient pas l’élément dont on cherche le voisinage, afin d’éviter une boucle infinie : les constituants de cet ensemble sont appelés voisin. Pour un élément donné, il n’existe qu’un seul et unique voisinage.

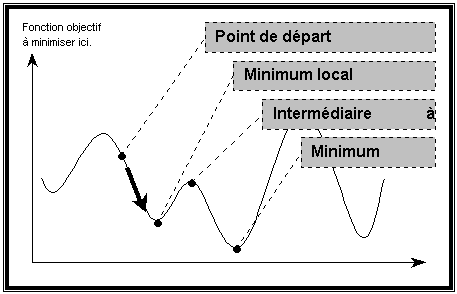Une fois que l’on a déterminé le voisinage, il faut savoir vers quel voisin de l’élément courant propager l’exploration. On doit donc faire un choix parmi tous ses voisins. Il faut noter que l’élément courant étant quasiment toujours modifié, le voisinage exploré est également différent à chaque itération. Si on prenait de manière systématique le meilleur voisin, à savoir celui optimisant la fonction objectif, on retomberait dans le cas d’algorithmes de descente ou « meilleur-d’abord », avec l’inconvénient cité précédemment : inefficacité face aux extremum locaux. Comme on peut le voir sur la figure, lorsque l’on se trouve en un extremum (minimum sur la figure) local, si l’on accepte pas d’emprunter un chemin intermédiaire non optimum, on reste enfermé dans cet optimum local, avec pour conséquence de ne pas découvrir d’autres optima locaux meilleurs voire l’optimum global.

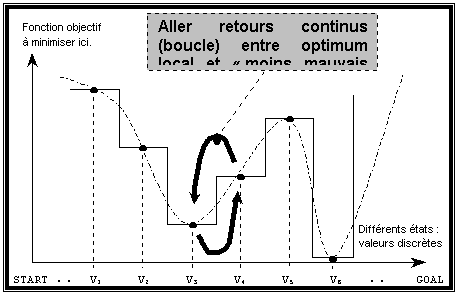Figure 4 : Sans mémorisation, risque de « bouclage »

Pour cela, deux techniques sont utilisées par les métaheuristiques:

·      l’introduction du hasard à donné naissance aux algorithmes de Monte-Carlo, à GRASP et au recuit simulé que nous allons voir dans le chapitre suivant.

·      L’introduction d’une mémoire flexible est à l’origine de la recherche tabou, que nous présenterons dans le chapitre d’après.

La première possibilité consiste donc à choisir un ou plusieurs voisins, sans examiner l’ensemble du voisinage. Cette sélection peut se faire soit par une heuristique, soit au hasard.

La seconde possibilité consiste à explorer l’ensemble du voisinage, et à sélectionner le (les) meilleur(s) élément(s). Encore une fois, le choix de l’élément peut se baser sur la valeur de la fonction objectif de cet élément, ou bien sur une heuristique.

Le hasard peut intervenir à plusieurs niveaux.

Tout d’abord, on peut choisir au hasard le prochain voisin que l’on va considérer. Cependant, l’intérêt du choix aléatoire, est d’éviter d’explorer et donc de générer tous les voisins. Plus que le choix, c’est donc véritablement la génération d’un voisin qui devra être aléatoire, sous entendu que le choix portera sur l’individu généré. Mais si les choix successifs étaient purement aléatoires, l’exploration de l’arbre de recherche le serait tout autant (random walk), est aurait peut de chance de trouver une solution, du moins de manière optimale : il faudra donc intégrer d’autres mécanismes pour rendre cette technique utilisable.

Mais le hasard peut intervenir à un autre niveau. Nous avons vu précédemment que pour ne pas s’enfermer dans un optimum local, l’algorithme devait être capable de passer par un voisin de « moins bonne qualité ». Mais comment déterminer la valeur de cette « moindre qualité » ?… Justement de manière aléatoire. En effet, on peut s’autoriser à passer par un voisin dont la valeur de la fonction objectif soit moins bonne que celle du nœud courant, en s’en écartant (au plus ou au moins) d’une valeur petite prise au hasard : c’est sur ce principe que fonctionne le recuit simulé.

Contrairement aux algorithmes d’énumération implicite comme A*, ceux que nous voyons dans ce chapitre n’utilisent pas de mémorisation systématique.

Le recuit simulé par exemple ne mémorise que l’état courant et le meilleur état trouvé.

Par contre, la recherche Tabou est basée sur une mémoire flexible[2] [Glov96], à savoir que l’on ne conserve que quelques informations nécessaires à l’exploration, soit concernant les éléments (cela peut demander beaucoup de ressources mémoires en cas de domaines étendus), soit concernant les mouvements, qui eux sont souvent en nombre déterminé ce qui permet de même de connaître à l’avance l’espace mémoire nécessaire.

Cette quantité d’espace mémoire nécessaire peut donc rapidement exploser. Pour limiter ce besoin, parfois problématique, on se base sur deux critères :

·      l’ancienneté[3] des éléments : en mémorisant l’instant d’apparition de l’élément on peut ensuite ne conserver que les n plus récents,

·      leur fréquence[4] : on mémorise ici le nombre de fois qu’intervient un élément ou un mouvement.

         Elle consiste à générer un nouvel élément, différent de ceux déjà explorés, dans le but de partir dans une nouvelle direction, pour explorer une autre région. Dans les algorithmes génétiques cette diversification porte le nom peut être plus explicite de mutation.

Partant de là, deux questions se posent :

·      quand lancer la diversification,

·      et dans quelle direction partir : à quoi doit ressembler le nouvel élément ?

Selon le but recherché et le problème considéré, plusieurs méthodes, permettant de déterminer à quel instant déclencher la diversification, s’offrent à nous.

La diversification peut tout d’abord être déclenchée de manière automatique. Le plus simple, consiste à déterminer un nombre de cycles, d’itérations, au bout duquel on déclenche la diversification.

De manière plus dynamique, pour ne pas dire « plus intelligente », on peut mettre en place une diversification basée sur le gel de l’exploration. En effet, dés que l’on détecte que les éléments générés demeurent (plus ou moins) constants, on peut lancer la diversification. Le moyen le plus simple là encore, est de se donner un nombre d’itérations de l’exploration, durant lequel cette fois la meilleure solution ne change quasiment plus, voire plus du tout.

Une dernière méthode envisageable, fondée sur la mémorisation, serait d’équilibrer l’apparition de diversités. En se basant sur les fréquences mémorisées, on peut percevoir l’apparition de nouveaux éléments, et lancer la diversification lorsque le déséquilibre devient trop grand, afin de garantir une certaine homogénéité : on cherche à explorer l’ensemble des éléments pas encore examinés de manière aussi uniforme que possible. Pour cela, dés qu’un ou plusieurs attributs dépassent une fréquence d’apparition (fixée ?), on détermine un nouvel élément courant excluant ces attributs très utilisés et privilégiant les attributs moins rencontrés jusqu'à présent. Cette dernière méthode apparaît comme un moyen de déterminer aussi bien l’instant où lancer la diversification que la direction dans laquelle s’engager.

Une fois que l’on a ainsi établi que la diversification devenait nécessaire, du moins utile, il reste encore à définir la forme du nouvel élément à générer. En d’autre termes, il faut déterminer la zone à explorée, délaissée jusqu’à là, qui permettrait la diversification de l’exploration. Expliciter cette notion de « zone », nous permettra de mettre en évidence les différentes méthodes envisageables. Une « zone » peut (doit ?) être vue comme un sous-ensemble de celui des éléments, non encore explorés et ayant des caractéristiques communes (mêmes valeurs pour des variables données…).

Si la méthode de détermination de l’élément initial n’est pas déterministe, à savoir si elle ne donne pas toujours le même père pour une instance donnée, on peut l’utiliser pour générer un nouvel élément ayant des caractéristiques proches de l’élément considéré, mais différent de lui.

Par contre, lorsqu’elle est déterministe, on peut la modifier en y introduisant une part de hasard dans la génération de l’élément, afin de différencier le nouveau successeur de l’ancien.

Une dernière méthode, serait d’utiliser la mémorisation des fréquences ou de l’ancienneté, comme déjà vu. Ainsi, au lieu de diverger vers une zone choisie de façon « hasardeuse » parmi celles délaissées, comme dans les deux méthodes précédentes, on considère la zone la plus délaissée. En classant les attributs ou les variables du problème selon les fréquences croissantes, ou les anciennetés décroissantes, on pourra ensuite utiliser une méthode gloutonne basée sur ce classement, c’est à dire construire un élément en privilégiant les attributs ou variables les mieux classés, donc les moins souvent rencontrés.

         L’idée générale de l’intensification, est pour ainsi dire complémentaire de la diversification, dans la mesure où elle vise à explorer préférentiellement une zone déjà examinée, et qui apparaîtrait comme prometteuse. La meilleure façon d’éviter une voie défavorable, n’est elle pas de s’engager vers une estimée comme prometteuse ? Cependant, cette technique est plus compliquée à mettre en pratique que la précédante. En effet, pour la diversification, il suffit de constater que la « qualité » du résultat est actuellement en deçà d’une valeur seuil pour s’engager vers une autre voie, alors que pour intensifier une zone, il faut être capable de prévoir si elle va être prochainement prometteuse.

Comme précédemment, plusieurs techniques permettent de déterminer quand lancer l’intensification.

On peut le faire de manière automatique, à savoir par exemple toutes les k itérations. Il s’agirait, au bout d’un nombre d’itérations donné, d’intensifier une zone à déterminer. Cette solution étant présente dans la littérature, je la reporte ici, mais je ne vois pas l’intérêt de considérer l’intensification autrement que de manière dynamique (et non automatique) à savoir par rapport à la qualité de la solution actuellement envisagée. Je pense en effet que si l’on se trouve sur une voie apparemment intéressante, ce serait pure perte de temps, et donc d’efficacité, que d’attendre que ce fameux nombre d’itérations soit atteint avant de décider d’intensifier.

Une autre (la !) solution est donc de se baser sur l'amélioration. L’intensification est dans ce cas déclenchée soit lorsqu’une amélioration de la meilleure solution est détectée, soit lorsque l’élément considéré prend la forme d’un schéma initialement défini comme prometteur.

Une fois que l’on a déterminé que la recherche devait être intensifiée, en plus de savoir quelle zone intensifier comme dans la diversification, il faut ici établir la durée de l’intensification, à savoir pendant combien d’itérations il faudra rester dans cette voie qui peut finalement s’avérer être non optimum.

Pour déterminer la zone à intensifier, la méthode la plus simple est la mémorisation. En effet, en comparant entre elles les n meilleures, ou les n dernières, solutions trouvées précédemment, et enregistrées, on peut alors les comparer entre elles pour établir l’ensemble des attributs qu’elles ont en commun et qui définiront la zone à intensifier.

Une autre possibilité est de partir simplement d’une ancienne solution enregistrée, et d’imposer certains mouvements et/ou d’en interdire d’autres, pendant un certain temps, de façon à favoriser l’exploration intensive de la zone ainsi déterminée par contraintes autour de l’ancienne solution.

Reste encore à déterminer le nombre d’itérations pendant lequel on s’autorise à rester dans cette zone soit disant prometteuse avant d’atteindre éventuellement une solution.

Cette étape est particulièrement importante et délicate. En effet, il faut ici établir le nombre d’itérations pendant lequel on va s’investir dans l’intensification. Rappelons que le caractère « prometteur » de la voie empruntées n’est forcement qu’une estimation. Par conséquent, avant d’arriver à la solution, il va falloir réaliser un certain nombre d’itérations. Le problème tient au fait que cette voie empruntée peut finalement s’avérer être une impasse infructueuse, et donc une perte de temps d’autant plus grande que le nombre d’itérations était important. Ainsi il faudra donc faire un compromis entre le degré de certitude avec lequel l’algorithme est capable de déterminer si une solution est prometteuse, et le temps à lui consacrer : si l’algorithme est capable de déterminer avec précision que la voie est prometteuse, on peut s’autoriser un plus grand nombre d’itérations avant d’obtenir la solution, puisqu’on est quasiment sûr d’obtenir une (bonne) solution. La détermination de la durée de l’intensification peut être faite :

·      soit de façon préalable et statique : mais déterminer de manière statique quand arrêter l’intensification apparaît tout aussi inefficace que de déterminer de la même façon quand la commencer (Cf. un peu plus haut…),

·      soit en considérant le nombre d’itérations ayant été nécessaire pour établir les précédentes solutions,

·      soit en tenant compte du degré d’instanciation de la zone à intensifier et du nombre de mouvements imposés,

·      soit en étant attentif aux variations de la qualité de la solution considérée,

·      soit enfin en mixant tout cela…

En fait, il apparaît que les critères et techniques de détection de la date où commencer, et de celle où terminer l’intensification, sont similaires.

         L’oscillation consiste à s’approcher d’une frontière, à la dépasser, puis à en s’en éloigner, avant de faire demi tour et de recommencer.

L’intérêt de cette technique apparaît lorsque la caractéristique (courbe) de la fonction objectif est fortement indentée. On peut ainsi sauter de proche en proche, d’extrema locaux en extrema, en s’affranchissant des nombreux « mauvais » voisins.

Pour cela :

·      soit on modifie la fonction objectif (on « leurre » l’algorithme),

·      soit on force la direction d’exploration dans le voisinage, obligeant ainsi à poursuivre la recherche malgré les « mauvais » voisins.

Cette technique dégage plusieurs avantages, notamment présentés dans [KGA93] et [Glov89].

·      Si le graphe associé aux éléments réalisable n’est pas connexe, à savoir s’il possède au moins deux éléments non reliés entre eux par un chemin, alors l’oscillation permet de traverser les zones non réalisables au cours de la recherche. De plus, même si le graphe est connexe, mais que les chemins soient long et tortueux, l’oscillation permet là encore de « prendre comme raccourci » un « mauvais » voisin.

·      Pour certains problèmes, le simple fait de trouver une solution est déjà une problématique NP-complet : dans ces conditions ne parlons donc pas de trouver une solution optimum. L’oscillation peut permettre dans ces cas une définition et une exploitation plus simple, voire utilisable, du voisinage.

·      Enfin, pour couvrir une zone la plus large possible, et favoriser ainsi au maximum la découverte de solutions éventuelles, et donc être d’avantage efficace, les techniques d’exploration locale doivent assurer une diversité suffisante en ce qui concerne les éléments observés. L’oscillation fourni cette diversité révélant ainsi des possibilités d’amélioration inaccessibles lorsque l’exploration est restreinte à des zones plus réduites.

Exemple d’exploration locale : Le Recuit Simulé

         Les origines de la méthode du Recuit Simulé[5] remontent aux expériences de Metropolis et al. [MRRT53]. Leurs travaux ont abouti à un algorithme simple pour simuler l’évolution d’un système physique instable vers un état d’équilibre thermique à une température T fixée. Un état de ce système est caractérisé par la position exacte de l’ensemble des atomes qui le constituent. Tout nouvel état est obtenu en faisant subir un déplacement infinitésimal et aléatoire à un atome quelconque. Soit ΔE la différence d’énergie occasionnée par une telle perturbation. Le nouvel état est accepté si l’énergie du système diminue (ΔE < 0). Dans le cas contraire, il est accepté avec une certaine probabilité.

De nombreuses années se sont écoulées depuis les travaux de Metropolis et al. avant que leur algorithme soit exploité en 1983 par Kirkpatrick [KGV83] en vue de définir une nouvelle heuristique pour l’optimisation combinatoire. En faisant l’analogie entre l’énergie du système physique et la fonction objectif du problème d’une part, et entre les états successifs du système et les solutions admissibles d’autre part, en considérant de plus la température d’un système physique ne terme d’agitation thermique, et en s’inspirant de la méthode de Monte-Carlo, le recuit simulé consiste donc à chaque itération à choisir aléatoirement un voisin dans le voisinage de l’élément courant, et à le considérer comme le nouvel élément courant:

·      avec certitude s’il est de meilleur qualité,

·      avec une certaine probabilité, sinon.

Si f est la fonction d’évaluation ou objectif d’un élément (celle qui détermine sa qualité), v le voisin d’un élément donné u, et T la température courante, alors la probabilité associée à ce voisin pour la température T est définie comme suit :

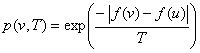
Dans le cas le voisin choisi est de moindre qualité, l’acceptation de ce dernier se fait en générant aléatoirement un nombre compris entre 0 et 1 exclu. Si ce nombre est inférieur ou égale à la probabilité affectée au voisin alors ce dernier est accepté, dans le cas contraire, on maintient l’élément courant.

Toute meilleure solution trouvée est mémorisée, et l’algorithme s’arrête lorsque plus solution n’est détectée parmi les voisins, pendant un pallier de température (cycle complet d’itérations à une température donnée, ou que la température est nulle).

Pour des présentations plus complètes et détaillés du recuit simulé, on pourra se reporter à [KGV83], [JAMS89], [Egle90] et [Dows93].

Afin que ces détériorations temporaires, mais successives, de la qualité soient contrôlées, le recuit simulé intègre un paramètre supplémentaire, appelé température, qui correspond à un écart maximum à partir de la solution courante, en dehors duquel les valeurs de la fonction objectif ne doivent pas s’aventurer. Les variations de cette température sont imposées de manière précise par une fonction décroissante appelée fonction de refroidissement. En règle générale, la température est diminuée par pallier, à chaque fois que l’on a effectué un nombre donné d’itérations. La nouvelle température est obtenue en multipliant l’ancienne par un coefficient a plus petit que 1 : a Î ]0, 1[ .

Se pose alors le problème de déterminer une valeur pertinente pour a. On peut déjà noter que a ne doit pas être trop loin de 1. En effet, d’après des travaux théoriques, l’algorithme converge si la température « lui en laisse le temps ». De manière pratique, entre chaque variation de température, il faut que l’algorithme ait l’« autorisation » (intervalle de recherche, ou température, assez grand) et le temps (suffisamment d’itérations pour chaque pallier) de balayer suffisamment de situations. Déterminer une valeur pertinente pour ce paramètre ne peut donc être fait de manière absolue, mais au contraire en corrélation avec le nombre d’itérations autorisées pendant chaque pallier (paramètre NB_MAX à la ligne 14 de l’algorithme).

Lorsque la température est abaissée suffisamment lentement pour que l’équilibre soit maintenu, le processus se traduit par une augmentation du poids des configurations à basse énergie.

Ainsi, à mesure que l’on progresse dans la recherche, la température diminue, et il en est de même pour l’importance des détériorations acceptées : l’exploration évolue d’une stratégie quasiment de type aléatoire au départ, vers une stratégie de type « meilleur d’abord ». Le nouvel élément est toujours pris au hasard dans un voisinage. Cependant, au départ la forte température implique que la dimension de ce voisinage est grande et que l’on choisi au hasard parmi des voisins divers et variés (tous les changements sont acceptés : la probabilité d’acceptation, étant de la forme exp(-k/T), tend vers 1 quand T est grand), alors que la faible température finale, synonyme de voisinage restreint, sous entend que les voisins disponibles sont proches de la solution actuelle (exp(-k/T), et donc la probabilité d’acceptation d’une solution plus mauvaise, tend vers 0 quand T est petit).

Voici l’algorithme du la méthode du Recuit Simulé.

1.          Fonction RS(u₀ : T_Element) : T_Element          // u₀: élément initial
2.              u ß u₀
3.              V(u₀) ß Determiner_voisinage_de(u₀)
4.              T ß T₀                                                                   // T0: température initiale
5.              CONDITION_D_ARRET ß faux
6.              NB_ITERATION ß 0
7.              Tant que (CONDITION_D_ARRET = faux) faire
8.                   CONDITION_D_ARRET ß vrai
9.                   Tant que (NB_ITERATION < NB_MAX) faire // NB_MAX itérations par T
10.                      NB_ITERATION ß NB_ITERATION + 1
11.                      v ß Choix_aleatoire_dans(V(u))
12.                      u_old ß u
13.                      Si (f(u) ≥ f(v)) alors                  // Si le voisin est meilleur
14.                           u ß v
15.                           CONDITION_D_ARRET ß faux
16.                      Sinon                            // Sinon calcule probabilité
17.                           p = Tirage_aleatoire_dans([0; 1])
18.                           Si (p < exp(-|f(v)-f(u)|/T)) alors
19.                                 u ß v
20.                                 CONDITION_D_ARRET ß faux
21.                           Fin_Si
22.                      Fin_Si
23.                      Si (u ≠ u_old) alors                    // cad si u a été modifié
24.                           V(u) ß Determiner_voisinage_de(u)
25.                      Fin_Si
26.                Fin_TantQue
27.                T ß Fonction_de_refroidissement(T)           // souvent: T ß a.T / 0<a<1
28.                CONDITION_D_ARRET ß CONDITION_D_ARRET ou (T = 0)
29.                                                       // Si T=0 on arrête aussi
30.           Fin_TantQue
31.           Retourner u

Tant que la condition d’arrêt n’est pas vérifiée (ligne 7), pour chaque pallier de température on fait NB_MAX itérations (ligne 9) où :

-         on choisit au hasard un élément dans le voisinage V(u) de l ‘élément courant noté u (ligne 11),

-         si le voisin est de meilleure qualité (ligne 13) on le prend comme nouvel élément courant (ligne 14),

-         sinon, on l’accepte selon les conditions des lignes 16 à 22 de l’algorithme.

-         si l’élément courant a été modifié (ligne 23), on calcule alors son voisinage (ligne 24), puis on passe à l’itération suivante.

Une fois le NB_MAX d’itérations effectuées, on diminue la température (ligne 27).

Si elle est alors nulle (pose notamment problème à la ligne 18 en divisant par zéro), ou que l’élément courant n’a pas été modifié durant le dernier pallier de température (lignes 28 et aussi 15 et 20), on arrète.

Il est à noter, que l’on peut trouver en lieu et place de « élément u » la notion de « solution s ». Plus qu’un simple changement de lettre, cela implique que l’on connaît au départ déjà une solution au problème, et qu’au lieu de chercher à extraire une solution on souhaite optimiser une solution déjà connue mais de « mauvaise » qualité au départ.

         Tout d’abord, l’utilisation d’une température, qui plus est variable, permet de prendre en compte des dégradations contrôlées des éléments, et ainsi de ne pas s’enfermer dans des optima locaux. Du points de vue théorique, le recuit simulé converge vers une solution optimale (il suffit de prendre une décroissance infiniment lente de la température[6]), et en pratique, présente des performance accrues par rapport aux méthodes de recherche du « meilleur d’abord » (algorithme A*) ou basée sur l’exploration purement aléatoire (Monte-Carlo).

Cependant, comme d’habitude, cette efficacité à un prix. En plus de la définition des voisinages, de la tolérance aux dégradations (la fonction donnée dans l’algorithme est la plus répandue, mais on en trouvera d’autres dans [Dows93] p. 43) et de la condition d’arrêt, il est nécessaire de définir de nombreux autres paramètres, définitions rendues délicates par les interactions existantes. Il s’agit plus précisément :

·      des températures initiale et finale ainsi que de la fonction de refroidissement (Cf. [Dows93] p.44),

·      de la longueur de chaque chaîne pour une température donnée (nombre d’itérations à cette même température).

En fait, la définition de ces paramètres correspond aux étapes de diversification,  d’intensification et d’oscillation, que nous avons étudiées dans le chapitre précédant. 

Elle dépend du type de problème traité, du type de résultat que l’on souhaite obtenir, de la forme des instances envisagées, et traduit le compromis entre la qualité souhaitée pour la solution finale, et la rapidité d’obtention de cette solution qui sera le plus souvent contraignante et imposée.

En effet, contrairement à d’autres heuristiques, il est impossible d’arrêter l’algorithme du recuit simulé avant la fin, car le refroidissement perd alors toute signification. Le fait de tolérer la sélection de « mauvais » éléments, qui plus est avec une grande part de hasard certes décroissante, dans le but d’atteindre plus rapidement la solution éventuelle, entraîne que l’algorithme passe par des phases « instables » susceptibles d’être la solution courante si l’on arrête l’exploration avant la fin. Cela confère une importance toute particulière au critère d’arrêt du recuit simulé, contrairement à d’autres techniques, comme les algorithmes génétiques par exemple, où l’évolution de la solution est monotone dans le sens de l’optimum : on peut donc extraire à tout moment une solution significative, même si sa qualité augmente avec la durée de l’exploration.

Mais cet inconvénient n’en est pas forcément un pour nous, selon ce que nous allons considérer comme élément du voisinage. En effet :

·      soit cet élément correspond à une séquence d’actions, initialement vide, que l’on construit et complète à mesure de l’exploration,

·      soit c’est une séquence qui dés le départ contient n actions, pouvant avoir aucune signification (extraction de solution) ou au contraire être consistante (optimisation de solution), et qui par ajout et/ou modification d’actions va évoluer vers une solution meilleure, voire optimale.

Dans le premier cas, il apparaît évident qu’arreter l’algorithme avant la fin n’a pas d’intérêt. Le problème est donc de savoir si l’on fait simplement de l’extraction ou si l’on part d’une solution existante dans le but de l’optimiser …

Dans la planification, les temps de traitement actuels s’envolent dés que le nombre d’actions possibles dépasse le millier. Dans ces conditions, il apparaît primordial de savoir tout d’abord extraire une séquence solution dans des délais acceptables, à défaut d’être optimums. A partir de là, étant donné le coût d’une optimisation, on en droit de se demander si elle serait intéressante compte tenu de l’amélioration apportée. Par exemple, si l’optimisation d’une séquence solution initiale de 1500 actions, produit une séquence meilleure (et même optimale) de 1300 actions, pour un temps équivalent à celui de l’extraction de la solution initiale, on peut éventuellement remettre en question son intérêt, et en tout cas certainement le relier au type du problème à planifier.

Autre exemple : La méthode Tabou

         Développée par Glover, [Glov89] et [Glov89], et indépendamment par Hansen sous le nom anglais de « steepest ascent, mildest descent », la Recherche Tabou[7] est une méthode séquentielle.

A l’inverse de celles présentées précédemment qui ne génèrent qu’un seul voisin, la méthode Tabou examine un sous-ensemble de solutions pour ne retenir que la meilleure. Dans certains cas où le voisinage n’est pas trop étendu, il est possible de l’examiner entièrement pour sélectionner effectivement LA meilleure solution, au lieu d’en choisir une aléatoirement parmi les meilleures comme cela se fait en présence de voisinages trop vastes pour être intégralement explorés.

         La recherche tabou génère donc de manière générale plusieurs solutions à chaque étape, ce qui risque de la faire boucler dés qu’elle s’éloigne d’un extremum local : la sélection du meilleur voisin provoquant au tour suivant le retour à l’extremum local que l’on va quitter. Pour prévenir cela, elle reprend la notion de diversification vue précédemment, à savoir l’interdiction de certains mouvements qualifiés alors de tabous afin de ne pas revenir à une solution déjà rencontrée récemment. Le caractère tabou d’un mouvement doit être temporaire afin d’accroître la flexibilité de l’algorithme par remise en question des choix effectués une fois les risques de cycle écartés.

Ainsi, à chaque itération, on mémorise dans une liste, qu’on appellera par la suite TABOU, l’élément u (ou solution s) courant(e). Désormais, les voisins autorisés d’un élément u sont tous ceux présents dans son voisinage privé de ceux obtenus à partir des mouvements contenus dans TABOU.

La gestion de ces listes, qui permettent à l’algorithme de mener une exploration aussi large que possible tout en réduisant les risques de bouclage, joue donc un rôle essentiel dans l’algorithme et la longueur de chacune d’entre elles doit être définie rigoureusement en fonction du problème considéré.

On pourra obtenir des présentations très complètes de la recherche tabou dans [Glov89], [Glov90], [GTD93] et [GlLa93].

Voici une première version simplifiée de l’algorithme de la Méthode Tabou.

1.        Fonction RT(u₀ : T_Element) : T_Element
2.             u ß u₀                                                       // u0: element initial
3.                u* ß u₀                                                     // u*: meilleur element trouvé
4.             TABOU ß Ø                            // liste(s) TABOU vide(s)
5.             CONDITION_D_ARRET ß false
6.             NB_ITERATIONS ß 0
7.             Tant que (CONDITION_D_ARRET = false) et (V(u; TABOU) ≠ Ø) faire
8.                  NB_ITERATIONS ß NB_ITERATIONS + 1
9.                  v ß Meilleur_element_de(V(u; TABOU))
10.                Si (f(v) ≥ f(u*)) alors
11.                    u* ß v
12.               Fin_Si
13.               Mise_a_jour_de(TABOU)           // voir paragraphe suivant
14.               u ß v
15.          Fin_TantQue
16.          Retourner u*

Une amélioration consiste à prendre en compte non pas une mais plusieurs solutions possibles, à intégrer dans les listes tabou des attributs de mouvements, et à utiliser la fonction d’aspiration.

17.     Fonction RT2(u₀ : T_Element) : T_Element
18.          u ß u₀                                                       // u₀: élément initial
19.          u* ß u₀                                                     // u*: meilleur élément trouvé
20.          TABOU_i ß Ø                           // listeS TABOU videS
21.          CONDITION_D_ARRET ß false
22.          NB_ITERATIONS ß 0                                 // compteur d’itérations
23.          MEIL_ITERATION ß 0                          // itération de u*
24.          Tant que (CONDITION_D_ARRET = false) faire
25.               NB_ITERATIONS ß NB_ITERATIONS + 1
26.               VOISINAGE ß Determiner_les_solutions(TABOU_i, FONC_ASPIRATION)
27.                           // on génère un ensemble de solutions u’=u Å a
28.                           // satisfaisant au moins une des 2 conditions :
29.                           //   * au moins un attribut de a n’est pas tabou
30.                           //   * f(u*) < A(f(u))
31.               u* ß Meilleur_element_de(VOISINAGE)
32.               Mise_a_jour_de(TABOU_i)           // voir paragraphe suivant
33.               Mise_a_jour_de(FONC_ASPIRATION) // voir paragraphe d’après
34.               Si (f(u) < f(u*)) alors
35.                    u* ß u
36.                    MEIL_ITERATION ß NB_ITERATIONS
37.               Fin_Si
38.                           // On s’arrête :
39.               CONDITION_D_ARRET ß (NB_ITERATIONS - MEIL_ITERATION > NB_MAX)
40.                           //     si ca fait au moins NB_MAX itérations
41.                           //     que l’on a pas modifié la meilleure solution
42.               CONDITION_D_ARRET ß CONDITION_D_ARRET ou (NB_ITERATIONS > NB_TOT)
43.                          //  OU si l’on a fait au total + de NB_TOT itérations
44.          Fin_TantQue
45.                     Retourner u*

Comme pour l’algorithme du recuit simulé, on peut trouver en lieu et place de « élément u » la notion de « solution s », avec les mêmes implications.

Cette mise à jour de TABOU, directement déterminée par sa structure et effectuée à la ligne 13 et 32 de l’algorithme,  peut être de complexité variable.

La façon la plus simple de faire, est de la considérer de manière circulaire, de type First In, First Out (FIFO). On ajoute en fin de liste l’élément courant, et on retire le premier élément de la liste qui correspond en fait au plus ancien. Cette gestion permet d’éliminer assurément tous les cycles de longueur inférieur ou égale à ||TABOU|| (nombre d’éléments dans TABOU). Ainsi tous les éléments tabous ont la même longévité et demeurent interdit pendant le même nombre d’itérations, à savoir ||TABOU||.

Une autre approche serait d’attribuer cette fois à chaque mouvement tabou un nombre d’itérations qui lui soit propre. On pourrait donc former TABOU de couples constitués :

·      du mouvement que l’on vient de considérer (entre un élément u et son voisin v),

·      et d’une valeur n, propre à chaque mouvement, et qui correspond au nombre d’itérations pendant les quelles ce mouvement restera interdit.

·      Cette variante n’a réellement d’intérêt par rapport à la précédente que si les n sont différents pour chaque mouvement. La mise à jour de TABOU consiste alors à décrémenter pour chaque mouvement présent dans la liste, le nombre d’itérations associé, et à supprimer les couples dont ce nombre est nul. Il faut maintenant se demander si la souplesse assurée ici est bien intéressante au vu du traitement supplémentaire (parcours de toute la liste…) qu’elle occasionne.

On peut également envisager des gestions de listes TABOU plus complexe où les durées d’interdiction, c’est à dire le nombre d’itérations pendant lesquelles un mouvement restera interdit, peuvent être variées comme précédemment, mais aussi variables comme dans les listes dynamiques de [DaVo93]. Ainsi, chaque mouvement possède une durée d’interdiction propre, qui peut cette fois changer pendant l’exécution de l’algorithme. Il faut alors déterminer quel mouvement considérer, puis quelle valeur lui assigner en fonction d’une règle initialement définie, ou en fonction des caractéristiques des éléments considères, ou encore de manière aléatoire dans un intervalle donné.

Cependant, de telles démarches peuvent devenir rapidement très coûteuses en temps de calcul et en place mémoire suivant le type des éléments considérés. Une alternative efficace consiste à mémoriser certains attributs du mouvement considéré (pour passer de u à son voisin) plutôt que le mouvement lui même. Ainsi, dans les étapes suivantes, un mouvement quelconque sera interdit si tous ses attributs sont présents dans les listes, selon la nature et le nombre de ces mêmes attributs. Ce gain de mémoire ne sera efficace que si l’on est capable de sélectionner de manière pertinente les « bons » attributs .

Mais dans tous les cas, il est nécessaire de déterminer avec précision des valeurs pertinentes pour la longévité des mouvements tabous ou de leurs attributs: trop longue elle endommagerait l’efficacité de l’algorithme en rendant éventuellement le problème insoluble (chaque action ne pouvant alors être utilisée qu’une fois, le nombre d’action possibles diminuerait à chaque itération jusqu'à devenir éventuellement nul), et trop courte elle augmenterait les risques de cycle.

Il pourrait donc être utile d’avoir la possibilité de modifier le caractère tabou d’un mouvement…

         Cette notion intervient aux lignes 26 et 33 de l’algorithme.

La méthode Tabou est un cadre souple permettant d’incorporer toutes sortes d’améliorations et de méthodes avancées. Une des plus souvent retenues est le critère d’aspiration qui permet de passer outre certains interdits. Son utilisation principale consiste à outrepasser l’interdiction d’un mouvement s’il permet d’obtenir un élément meilleur que la solution trouvée jusqu’à présent.

Les listes tabou, surtout quand elles font intervenir des attributs d’éléments, peuvent générer des interactions pouvant accroître le pouvoir « tabou » des listes, et alors restreindre inutilement voire à tort l’ensemble des solutions autorisées à chaque itération. Dans certains cas, elles interdisent non seulement le retour aux dernières solutions visitées mais également tout un ensemble de solutions dont plusieurs peuvent ne pas encore avoir été visitées, et qui pourtant peuvent très bien être attrayantes voire meilleures que celles rencontrées jusqu’à là.

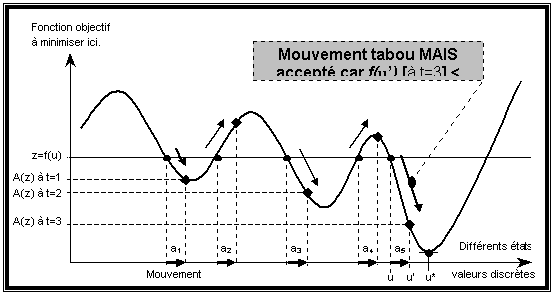
Cela étant, il est nécessaire de pouvoir modifier, et plus précisément supprimer, le caractère tabou d’une action, en particulier quand son application à l’élément courant peut conduire vers une solution estimée intéressante, mais sans augmenter le risque de cyclage dans le processus de recherche. Ce rôle est attribué à une fonction auxiliaire appelée fonction d’aspiration et notée A(). En général, son domaine de définition est constitué des valeurs que retourne la fonction objectif, notées z = f(u), pour tous les u déjà connus. Un z donné correspondant à une valeur fixée de f, il se peut que ce même z corresponde à plusieurs éléments u, pour peu que ces éléments aient la même valeur de fonction objectif : le nombre de z est donc inférieur ou égal à celui d’éléments u.

Le nombre A(f(u)) est appelé degré d’aspiration de f(u), et représente un seuil maximum, en dessous (si le but est de MINIMISER la fonction objectif) duquel l’algorithme est assuré de ne pas cycler lorsqu’il considère un élément v telle que f(v) = f(u).

Une action (mouvement) interdite a sera acceptée malgré tout si la condition d’aspiration suivante est satisfaite :

f(uÅa) < A(f(u)).[8].

La fonction d’aspiration A peut être définie de plusieurs manières.

L’une d’entre elles, est de définir pour chacun des éléments z = f(u) de son domaine de définition, la valeur de retour A(z) comme égale à f(u’) où u’ est la meilleure des solutions parmi toutes celles obtenues précédemment à partir d’un élément  ayant la même valeur de la fonction objectif, mais au coup suivant, après qu’il ait subit son action. Pour toute valeur de retour f(u) de la fonction objectif, A(f(u)) indique donc la meilleure valeur (de retour de la fonction objectif) rencontrée jusqu’à présent à l’itération suivante, c’est à dire une fois appliquée l’action ou modification.

En posant initialement pour tout z, A(z)=z, on mettra ensuite cette fonction d’aspiration à jour de la manière suivante :

A(f(u)) = min( A(f(u)) ; f(u’) )

A(f(u’)) = min( A(f(u’)) ; f(u) )

Cette définition de la fonction d’aspiration implique que les valeurs de la fonction objectif soient en nombre fini. Dans le cas contraire, on pourra étendre cette définition en prenant comme paramètre de la fonction A non pas des éléments z, mais des intervalles [z₁, z₂].

Ainsi, bien qu’on parle de FONCTION d’aspiration, il s’agira dans l’algorithme plus précisément d’une liste contenant les valeurs A(f(u)). Etant donné que nous avons un nombre fini d’éléments u (états du système) et que de plus f() est surjective (plusieurs antécédents u pour une même valeur résultat), on est assuré que notre liste sera de dimension finie et raisonnable.

Là encore la diversité est reine.

En règle générale, pour interrompre l’algorithme, on prend en compte deux critères. Tout d’abord on vérifie à chaque itération que le compteur d’itérations totales n’a pas dépassé un nombre maximal noté NB_TOT depuis le début du processus (Cf. ligne 42 de l’algorithme).

On se base sur une autre valeur seuil, NB_MAX, qui correspond au nombre maximal d’itérations que l’on s’autorise entre deux modifications (améliorations) consécutives de la (meilleure) solution (Cf. ligne 39 de l’algorithme).

Mais au lieu de considérer le nombre d’itérations, on pourrait aussi se baser sur le temps total, qui devrait être inférieur à une valeur maximale.

         Si l’algorithme de base de la méthode tabou est facile à implémenter, le nombre d’études menées sur cet algorithme, ses applications, ses améliorations possibles et les divers mécanismes qui peuvent lui être adjoints sont tels qu’il devient difficile de savoir quelles sont les options à retenir pour une implémentation particulière. En envisageant seulement le problème de la gestion de la liste tabou, des critères d’aspiration et des processus d’intensification et de diversification vus plus haut (sans compter la détermination du voisinage et de la condition d’arrêt), on se retrouve face à une grande combinaison de choix dans laquelle il est difficile de faire le tri.

Le plus souvent, il s’agit de principes très généraux qui laissent donc beaucoup de liberté dans leur application, mais qui nécessitent un important travail de mise au point de l’implémentation et de paramétrage pour obtenir des performances satisfaisantes. Ce travail n’est donc réellement effectué que lorsque l’implémentation de la méthode de base ne sonne pas de résultats satisfaisants ;

         De plus, contrairement au recuit simulé, il n’y a pas de résultats théoriques qui garantissent la convergence de la méthode Tabou vers une solution optimale. Celle ci étant en effet hautement adaptative et modulable, son analyse par des outils mathématiques traditionnels est malaisée. Cependant, à condition de modifier la fonction objectif et les probabilités de génération, certains résultats montrent que la méthode Tabou converge, mais après un temps infini ce qui serait justement ce qu’on cherche à éviter ! De toute façon l’important n’est pas de trouver la solution optimale, mais de visiter au moins une solution de bonne qualité au cours de la recherche.

Conclusion

L’avantage de ces méthodes est assurément leur généricité. En effet, elles peuvent être appliquées à un grand nombre de problèmes réduisant ainsi la tache de développer entièrement un algorithme au « simple » fait d’adapter l’heuristique (existante) au problème considéré. Cependant, cet avantage a son revers de la médaille : ces méthodes ne sont pas optimales, puisque non adaptées structurellement au problème. Surtout que pour certaines d’entre elles, les adapter de façon efficace au problème considéré peut finalement s’avérer au moins compliqué: leur structure repose souvent sur l’utilisation de paramètres supplémentaires (par exemple la température pour le Recuit Simulé ou encore le degré d’aspiration pour la méthode tabou) pour lesquels il est nécessaire de déterminer des valeurs pertinentes, afin de rendre l’algorithme efficace et donc justifié, ce qui n’est pas forcément d’une grande simplicité !

De plus, certaines de ces techniques ont un véritable intérêt lorsque les arrêtes reliant les nœuds ou états ont des valuations distinctes.

Par exemple dans le cas du voyageur de commerce, les arrêtes représentant la distance entre deux villes (les deux nœuds extrémités), le but est de trouver un chemin, de profondeur connue et constante (le nombre de villes à visiter), de manière à obtenir un ensemble (séquence) d’arêtes de coût total minimum. Un état est donc une séquence de villes, une DES villes. Le nombre de ville étant constant et le but étant de n’y passe qu’une fois, toutes les séquences envisagées ont un même nombre d’éléments (villes).

Par contre, dans la planification, deux nœuds représentent deux situations (ensemble de propositions) voisines. Une arrête correspond à l’action qui permet de passer d’une situation à une autre. La valuation de l’arrête est donc le coût de l’action, tous égaux. Dans l’anomalie de Sussman par exemple, toutes les actions ont la même « importance » : cout(A:BàC) = cout(B:AàTable) = ... .

Dans la planification, c’est donc la profondeur qu’il faut minimiser, les valuations étant égales, il faut le faire en un minimum d’itérations. Ces techniques aurait donc un intérêt réel si les actions possibles avaient des coûts distincts. Par exemple, il est préférable (de coût moindre) de soulever et déplacer une caisse vide plutôt qu’une caisse pleine.

Dernière Mise à jour: 26/08/2001

Accueil > Intélligence Artificielle > Méta-Heuristiques & Algorithmes de Recherche Locale